Quant Basics 10: Performance Prediction With Machine Learning
In the previous post we plotted a response surface of our strategy parameters and their PnL in order to assess if our choice of parameters is rational and not just a local maxima, which rapidly drops off as we move away from it. In this section we investigate how we can use machine learning to predict the performance of our parameter sets in order to save time in our parameter sweep.
You might recall that we’ve done the parameter sweep using Monte-Carlo parameter selection in order to quickly get a uniform coverage of our parameter space. If we would use a systematic sweep the coverage of the parameter space would gradually increase but we would need to wait for the entire sweep to finish for 100% coverage.
So, let’s assume we just backtested a small subset of our parameter space, like so:
pnls1,sharpes1,ddwns1,pnls2,sharpes2,ddwns2,params = run_parameter_sweep(tickers,start,end,BACKEND,5000)
This will cover approximately 15% of our total number of parameters as we specified the in this previous post. We can now feed these parameters into a machine learning algorithm and very quickly predict the performance of the other parameter sets. Luckily, this is easily done with sklearn and on top of that we can try different machine learning tools to see which one is the most appropriate. First, let us import some machine learning algorithms:
from sklearn.svm import SVR from sklearn.linear_model import LinearRegression from sklearn.tree import DecisionTreeRegressor
As you can see, we use linear regression, support vector machines and decision trees. For the two latter, we implement their regressor functions since we are looking for a continuous output, our PnL. Next, we fit our data using different models:
def predict_pnl(params, pnls1):
# model = SVR()
# model = LinearRegression()
model = DecisionTreeRegressor()
M = 25000 # M-len(params) is the number of parameter sets used for training
model.fit(np.array(params)[:-M,:],pnls1[:-M])
pred_pnls = model.predict(np.array(params)[:,:])
All we need to do here is uncomment the model that we intend to use. Let’s start with a linear regression. Remember that in our parameter sweep here, we ran 30,000 strategy parameter permutations. We now train our model on 5000 of them and then predict then see how well our model is able to predict the whole set of 30,000. Ideally, we should see a very good correlation between predicted and actual PnL. We can plot this with the code below.
plt.plot(pnls1[-M:],pred_pnls,'o')
m = plot_linreg(pnls1[-M:],pred_pnls)
plt.title('slope: %s'%m[0])
plt.xlabel('real PnL')
plt.ylabel('predicted PnL')
plt.show()
Cleary, the graph below shows that a linear model is not very well suited for this task. Using a non-linear model such as a support-vector-machine (SVM) should hopefully improve things a bit. We can do this simply by uncommenting the SVR() line in the code above and commenting out the linear regression line.
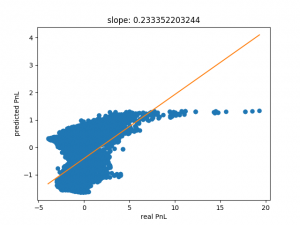
As you can see below, the performance is somewhat better but far from satisfactory.
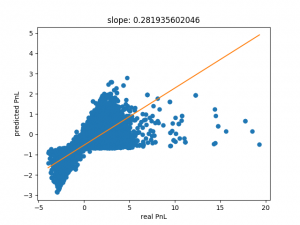
The SVM prediction clearly improves if we use half our data set (15000 points) as shown below but we still have an issue with the fact that our regression slope is far from one, as we would expect for a decent prediction.
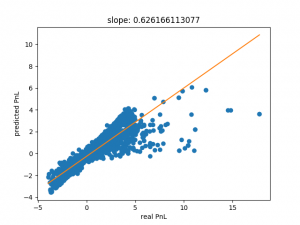
Decision trees can often fit data very well but have a tendency to overfit as well. Going back to our set with 5000 points of training data, we get the following result:
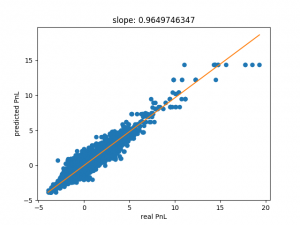
This is far more along the lines of what we would expect. Note, that the slope is also close to one. Using only 5000 point we can be quite confident that this is not overfitting.
Decision trees are quite good when the parameter sets we try to predict lie within the bounds of our parameter space. Since we used a Monte-Carlo sweep we can be reasonably sure that this is the case. However, decision trees are not very good for extrapolating any predictions with parameters outside the bounds of the parameter space. Linear models, if applicable at all, will usually do a better job with this.
Now, we have an efficient method to scan the parameter space quickly and find interesting regions. Finally, let’s plot the relation between the predicted train and test PnL as we’ve previously seen here.
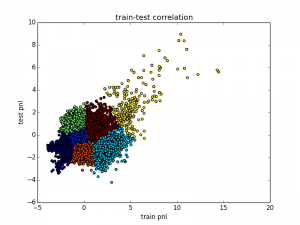
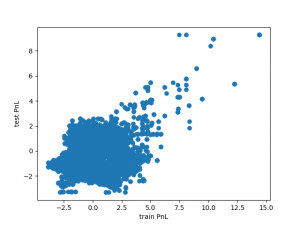
The left graph shows the original values from the actual backtests and the right graph shows the predicted behaviour. As we can see, the shape of the two graphs looks very similar even though we only used a small subset of our backtests for training the model.
This article has shown us an efficient way of reducing the number of backtests in a parameter sweep if we use a decision tree regressor to predict PnLs. This can save an enormous amount of time for our analysis.
Remember, the code base for this section can be found on Github.





11 Responses
Dear Tom,
I am impressed by your work. and the machine learning methodology to predict the pnls is quite eye-opening for me. However, I still have several unclear points to ask.
1. I understand that you can use ML to predict Pnl with parameter set. And in your code, you are using PnL from train dataset. But i cannot figure it out how you can come up with predicted train PnL and predicted test PnL (in the last chart). Are
Thanks again for sharing your invaluable experience with us.
Best regards
Hi Jianbo,
The idea is that if we have a very large parameter space we won’t be able to run through all possible parameter sets. So, In order to avoid that we simply train a machine learning model on a much smaller subset of the results and then we use that model to predict the PnL (or whatever metric) for other parameter sets which we have not backtested. These two lines do that:
model.fit(np.array(params)[:-M,:],pnls1[:-M])
pred_pnls = model.predict(np.array(params)[:,:])
In the previous blogs I have already calculated the PnL for every parameter set, so in order to make a point I am just using a subset of those when I train my machine. This is denoted with M. Originally we have 30000 parameter sets and setting M to 25000 means that we disregard that many and only use 5000 parameter sets.
I hope that makes sense. Please let me know if anything is still unclear.
Hi Tom,
Thanks your materials are awesome and the way you talk about your stuff is structured and easy to grasp. In your recent podcast you talked about sattelite images and you mentioned that some of these out of the box data is public and cheap, but hard to find. If it is not propriety, can you give an example on that data.
Is it something like analysing traffic cam records of main roads that connects port botany, counting the trucks and estimating the trade surplus?
I am always interested in using google trends data in my models, but concurrent seasonality adjustments made by abs is always outshadows the edge comes by google trends…
Hi Yigit,
There are a lot of really interesting info out there but you will have to do your own research to find them. Knowing where to find alternative data is one thing but actually incorporating them in models is another. As you said, there is a lot of difficulty in adjusting for things like seasonality and general noise. It seems that you already have some great ideas about using interesting data sets, I’m sure if you start digging you will find some more. All the best for your research.
Tom
Thanks Tom, have a great weekend.
Same to you, Yigit.
Hi Thomas,
thank you very much for explanation. I understand now the purpose of adopting ML for Pnl prediction.
However, I am wondering: since it looks promising to predict insample PnL (as your example), maybe it also works to use ML to predict directly out-of-sample PnL with inputs of parameter set and with/wo insample PnL.
If we can predict directly OOS PnL with all the in-sample information, and the strategy is ready: trade with the cluster of parameter sets which predict the highest OOS PnL. What do you thinK?
Another concern of applying ML is of-course over-fitting problem. I wonder how robust it is to use Random Forest to predict PnL.
Thanks again for your great help.
I’m not sure I would go as far as using this to predict OOS performance. It might work but that would also be lucky IMHO. Finding some correlation between IS and OOS is probably as far as I would go personally.
With regards to overfitting, in my example I show how using 5000 parameter sets can quite well predict the other 25000 using a simple decision tree. Random forest would just be a little bit more accurate I suppose, but I haven’t tried that yet. Let me know if you get some results there.
Hi Tom,
I just discovered your site after listening to your podcast. I get the sense that you are more interested in trading over larger time-frames with machine learning. I was wondering what your opinion is on using machine-learning for short-term trading. Do you think it would be easier to find positively correlated factors, but with weaker predictive power? Anyway, I’ve been reading your blogs and going through the code, and wanted to thank you for the time you’ve put in to make it human-readable.
I’ve also discovered this python repository recently, and I wonder if this project was integrated with your testing tools, and made publicly available for anyone to just run as a trading bot, how that would impact trading on those same time-frames? Would love to hear your opinion.
This is really interesting stuff, thanks!
Jagjot Singh
I forgot to link the repository mentioned in my previous comment:
https://github.com/pirate/bitcoin-trader
Hi Jagjot,
It is definitely possible to use pure machine learning for short-term trading but as far as my experience goes, it’s not easy to find tradable algorithms. Finding factors is not strictly machine learning, in my opinion but that’s a matter for a different debate. There’s definitely decent short-term factors that can be used.
I’ve had a quick look at the bitcoin trader repo you’ve mentioned. Of course you could use anything with analysis tools but you have to ask yourself if it makes economic sense. I’m not sure technical trading makes sense for bitcoin. This is something you need to research. Also, for this to work you need a lot of historical data.
Comments are closed.